SciML for power systems

Developing Scientific Machine Learning (SciML) methods for power system applications.

Abstract

In this project we developed a range of scientific machine learning (SciML) methods for surrogate modeling of electric power system dynamics and decision problems.

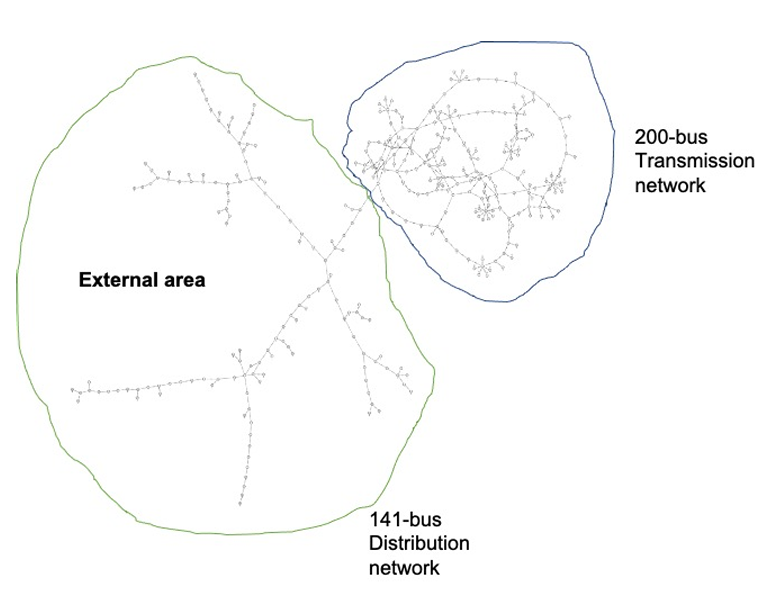
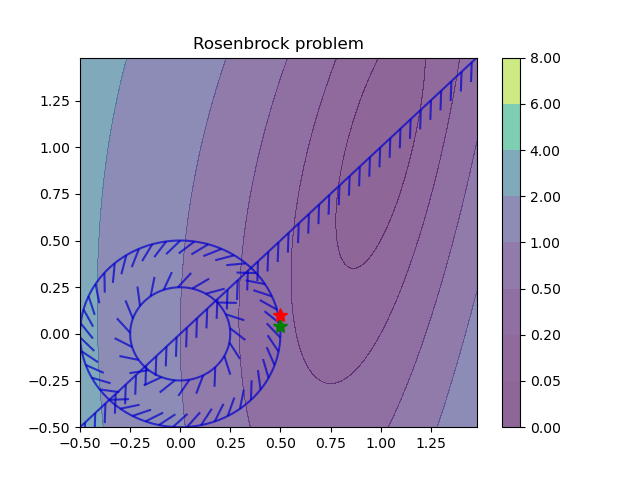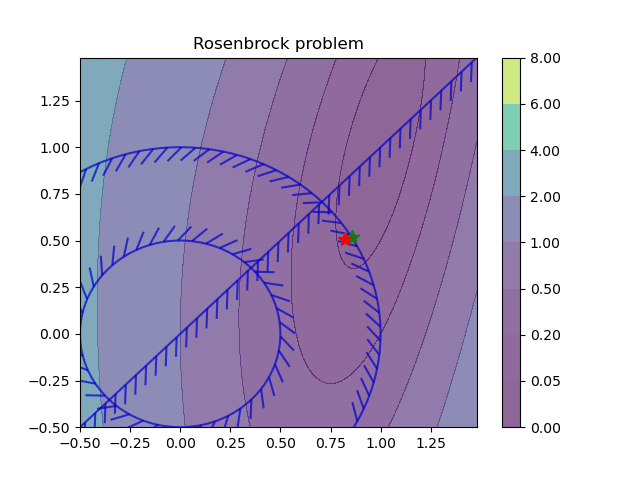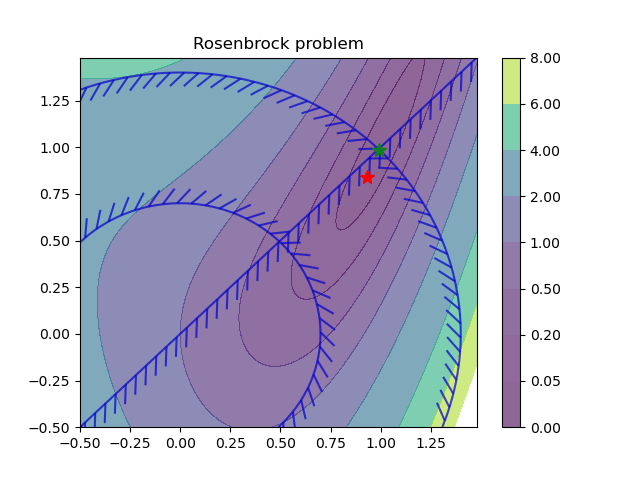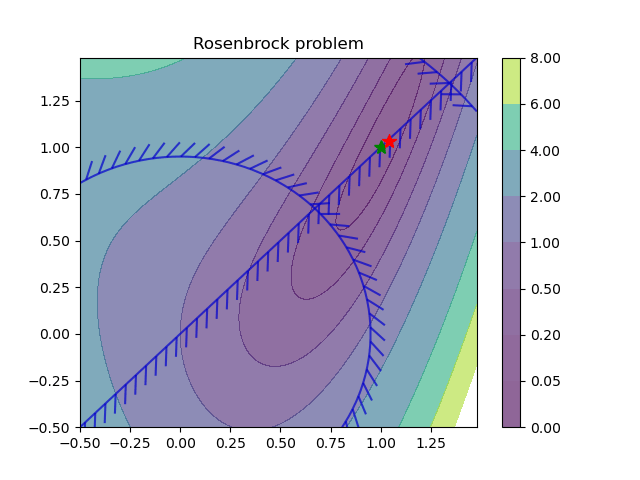
Learning to optimize: We have investigated the use of differentiable parametric optimization also called learning to optimize (L2O) approach to tackle several constrained optimization-based decision problems in power systems, namely load modeling of a transmission-distribution network, and optimal power flow (OPF) problem.

Imitation learning VS end-to-end learning using Differentiable Parametric Programming.

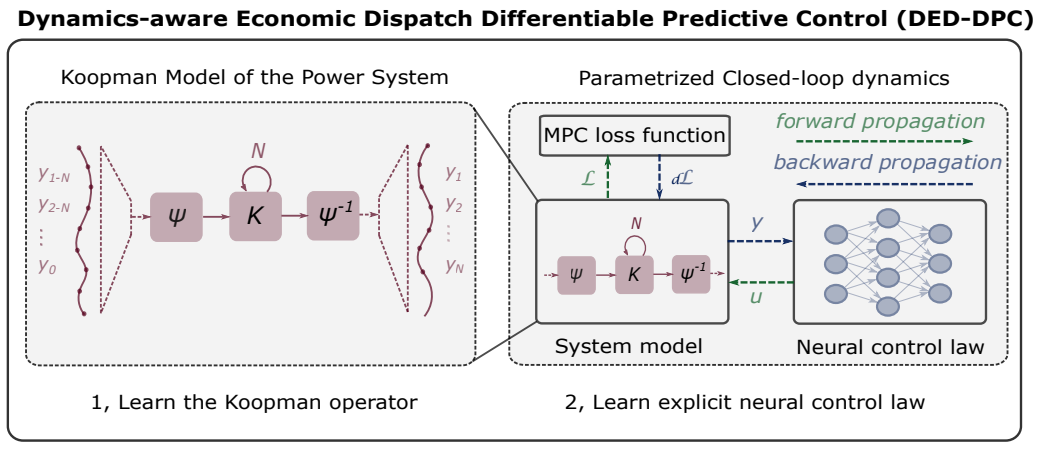
Learning to control: The dynamics-aware economic dispatch (DED) is an important problem in power systems that includes generator dynamics and operational constraints to enable near real-time scheduling of generation units in a power network. However, the incorporation of differential equations that govern the system dynamics makes this optimization problem computationally prohibitive to solve. To adress this limitation, we developed a novel method to employ the recently proposed differentiable predictive control (DPC) for offline learning of explicit neural control policies using an identified Koopman operator (KO) model of the power system dynamics. By doing so, we demonstrate the high solution quality and five orders of magnitude computational-time savings of the DPC method over the original online optimization-based DED approach.

Constructing a surrogate model of generator swing dynamics with a Koopman operator (KO) approach and leveraging differentiable predictive control to learn a solution map from forecast system loads to a schedule of generation inputs that meets the loads at least cost.

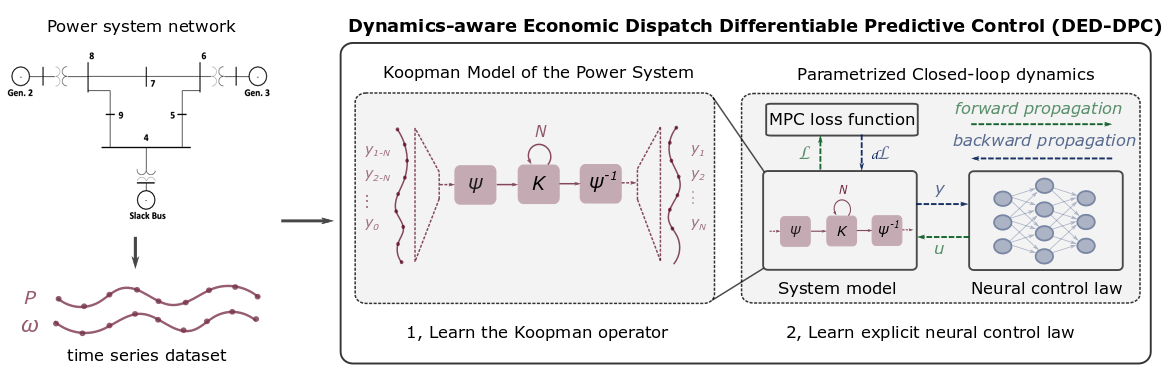
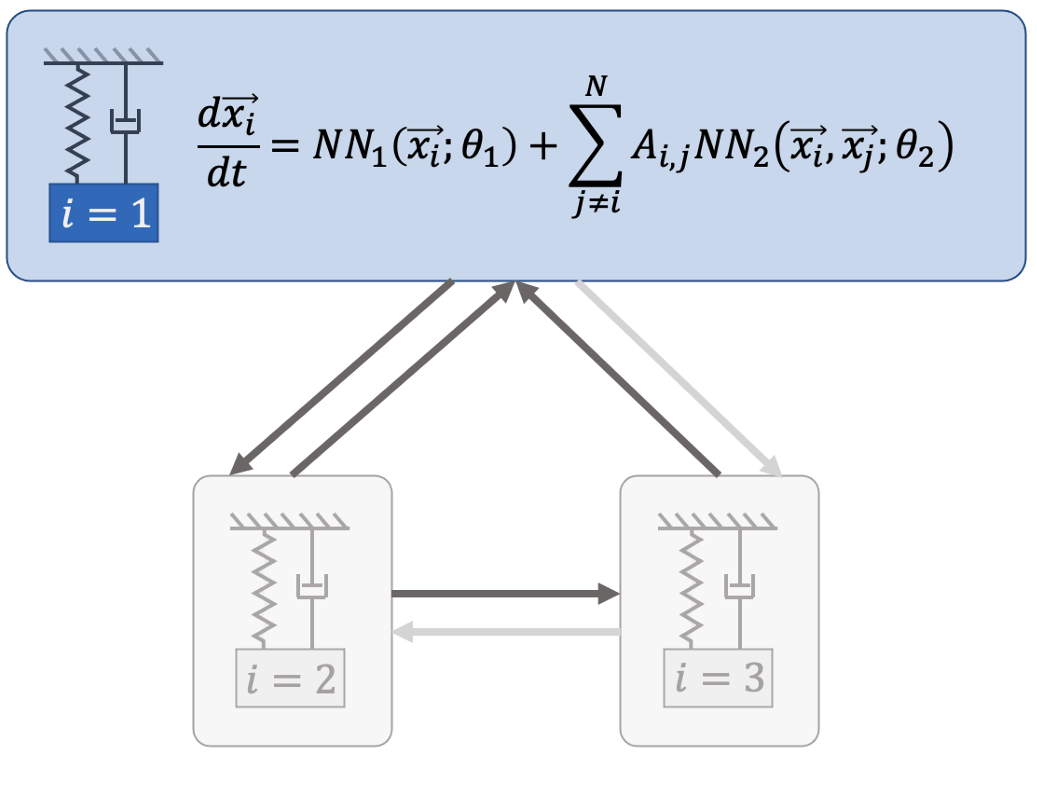
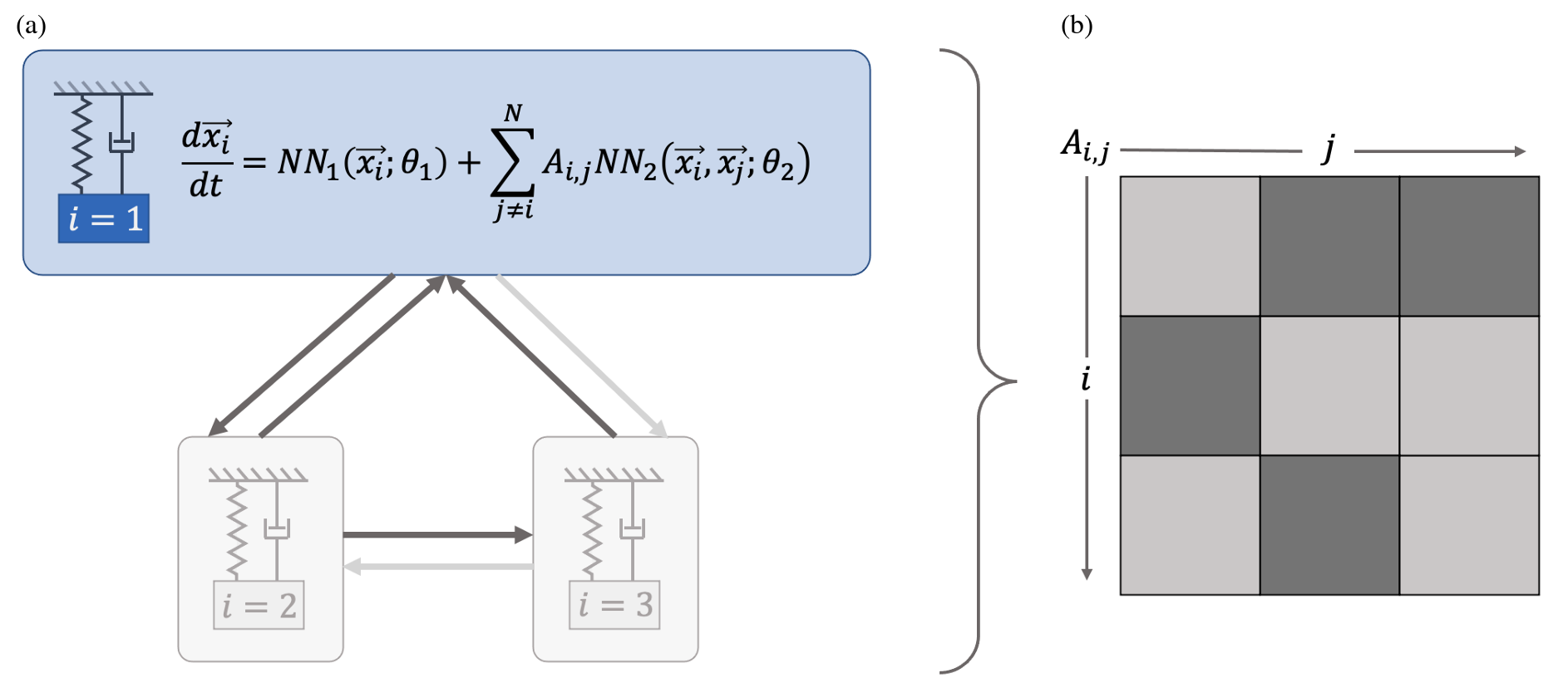
Modeling networked dynamical systems: Networked dynamical systems are common in power systems, however, they are notoriously hard to model with purely data-driven approaches. In our work, we seek to infer (i) the intrinsic physics of a base unit of a population, (ii) the underlying graphical structure shared between units, and (iii) the coupling physics of a given networked dynamical system given observations of nodal states. These tasks are formulated around the notion of the Universal Differential Equation, whereby unknown dynamical systems can be approximated with neural networks, mathematical terms known a priori (albeit with unknown parameterizations), or combinations of the two. We demonstrate the value of these inference tasks by investigating not only future state predictions but also the inference of system behavior on varied network topologies.

Conceptual methodology of networked dynamical system modeled via universal differential equations. In (a), a small network of unknown oscillators interact according to an adjacency matrix shown in (b).

Datasets: Our team lead by researchers form Carnegie Mellon University (CMU) also investigated power grid behavioral patterns in real-world datasets, including the time-varying topology, load, and generation, as well as the spatial differences between individual loads and generations. Based on these observations, we evaluated the generalization risks in some existing ML works caused by ignoring these grid-specific patterns in model design and training.

Open-source Software

The methods developed under this project is being open-sourced as part of the Neuromancer Scientific Machine Learning (SciML) library developed by our team at PNNL.

Acknowledgements

This research was supported by the Data Model Convergence (DMC) initiative via the Laboratory Directed Research and Development (LDRD) investments at Pacific Northwest National Laboratory (PNNL). PNNL is a multi-program national laboratory operated for the U.S. Department of Energy (DOE) by Battelle Memorial Institute under Contract No. DE-AC05-76RL0-1830.

PNNL Team

Ján Drgoňa (PI)
Shrirang Abhyankar (Co-PI)
Aaron Tuor
James Koch
Draguna Vrabie
Ethan King
Andrew August
Shimiao Li (CMU - Summer internship)

References

2023

Neuro-physical dynamic load modeling using differentiable parametric optimization

Shrirang Abhyankar, Ján Drgoňa, Aaron Tuor, and 1 more author

In 2023 IEEE Power & Energy Society General Meeting (PESGM), Jun 2023

Bib HTML

@inproceedings{10253098,
  author = {Abhyankar, Shrirang and Drgoňa, Ján and Tuor, Aaron and August, Andrew},
  booktitle = {2023 IEEE Power & Energy Society General Meeting (PESGM)},
  title = {Neuro-physical dynamic load modeling using differentiable parametric optimization},
  year = {2023},
  volume = {},
  number = {},
  pages = {1-5},
  doi = {10.1109/PESGM52003.2023.10253098},
}

ACM e-Energy
Power Grid Behavioral Patterns and Risks of Generalization in Applied Machine Learning

Shimiao Li, Ján Drgoňa, Shrirang Abhyankar, and 1 more author

In Companion Proceedings of the 14th ACM International Conference on Future Energy Systems, Jun 2023

Abs Bib HTML

Recent years have seen a rich literature of data-driven approaches designed for power grid applications. However, insufficient consideration of domain knowledge can impose a high risk to the practicality of the methods. Specifically, ignoring the grid-specific spatiotemporal patterns (in load, generation, and topology, etc.) can lead to outputting infeasible, unrealizable, or completely meaningless predictions on new inputs. To address this concern, this paper investigates real-world operational data to provide insights into power grid behavioral patterns, including the time-varying topology, load, and generation, as well as the spatial differences (in peak hours, diverse styles) between individual loads and generations. Then based on these observations, we evaluate the generalization risks in some existing ML works caused by ignoring these grid-specific patterns in model design and training.
@inproceedings{Shimiao2023, author = {Li, Shimiao and Drgoňa, Ján and Abhyankar, Shrirang and Pileggi, Larry}, title = {Power Grid Behavioral Patterns and Risks of Generalization in Applied Machine Learning}, year = {2023}, isbn = {9798400702273}, publisher = {Association for Computing Machinery}, address = {New York, NY, USA}, url = {https://doi.org/10.1145/3599733.3600257}, doi = {10.1145/3599733.3600257}, booktitle = {Companion Proceedings of the 14th ACM International Conference on Future Energy Systems}, pages = {106–114}, numpages = {9}, keywords = {domain knowledge, power grid, generalization, machine learning}, location = {Orlando, FL, USA}, series = {e-Energy '23 Companion} }
Structural inference of networked dynamical systems with universal differential equations

J. Koch, Z. Chen, A. Tuor, and 2 more authors

Chaos: An Interdisciplinary Journal of Nonlinear Science, Feb 2023

Abs Bib HTML

Networked dynamical systems are common throughout science in engineering; e.g., biological networks, reaction networks, power systems, and the like. For many such systems, nonlinearity drives populations of identical (or near-identical) units to exhibit a wide range of nontrivial behaviors, such as the emergence of coherent structures (e.g., waves and patterns) or otherwise notable dynamics (e.g., synchrony and chaos). In this work, we seek to infer (i) the intrinsic physics of a base unit of a population, (ii) the underlying graphical structure shared between units, and (iii) the coupling physics of a given networked dynamical system given observations of nodal states. These tasks are formulated around the notion of the Universal Differential Equation, whereby unknown dynamical systems can be approximated with neural networks, mathematical terms known a priori (albeit with unknown parameterizations), or combinations of the two. We demonstrate the value of these inference tasks by investigating not only future state predictions but also the inference of system behavior on varied network topologies. The effectiveness and utility of these methods are shown with their application to canonical networked nonlinear coupled oscillators.
@article{KochChaos2023, author = {Koch, J. and Chen, Z. and Tuor, A. and Drgoňa, Ján and Vrabie, D.}, title = {{Structural inference of networked dynamical systems with universal differential equations}}, journal = {Chaos: An Interdisciplinary Journal of Nonlinear Science}, volume = {33}, number = {2}, pages = {023103}, year = {2023}, month = feb, issn = {1054-1500}, doi = {10.1063/5.0109093}, url = {https://doi.org/10.1063/5.0109093}, eprint = {https://pubs.aip.org/aip/cha/article-pdf/doi/10.1063/5.0109093/16958339/023103\_1\_5.0109093.pdf} }

Homotopy Learning of Parametric Solutions to Constrained Optimization Problems

Shimiao Li, Ján Drgoňa, Aaron R Tuor, and 2 more authors

Feb 2023

Bib HTML

@misc{li2023homotopy,
  title = {Homotopy Learning of Parametric Solutions to Constrained Optimization Problems},
  author = {Li, Shimiao and Drgoňa, Ján and Tuor, Aaron R and Pileggi, Larry and Vrabie, Draguna L},
  year = {2023},
  url = {https://openreview.net/forum?id=GdimRqV_S7}
}

2022

Koopman-based Differentiable Predictive Control for the Dynamics-Aware Economic Dispatch Problem

Ethan King, Ján Drgoňa, Aaron Tuor, and 4 more authors

In 2022 American Control Conference (ACC), Feb 2022

Bib HTML Code

@inproceedings{9867379,
  author = {King, Ethan and Drgoňa, Ján and Tuor, Aaron and Abhyankar, Shrirang and Bakker, Craig and Bhattacharya, Arnab and Vrabie, Draguna},
  booktitle = {2022 American Control Conference (ACC)},
  title = {Koopman-based Differentiable Predictive Control for the Dynamics-Aware Economic Dispatch Problem},
  year = {2022},
  volume = {},
  number = {},
  pages = {2194-2201},
  url = {https://ieeexplore.ieee.org/abstract/document/9867379},
  doi = {10.23919/ACC53348.2022.9867379}
}