Decision and Control of Complex Systems

Developing scientific machine learning methods for modeling and control of complex systems.

Abstract

The objective of this project is to develop the mathematical foundations and framework for controlling and optimizing complex systems by developing novel scientific machine learning (SciML) methods. In US Department of Energy (DOE) mission areas, the analyses, simulations, and optimizations of these complex systems have been the objectives of numerous past research efforts. In this project, we recognize the fundamental challenge of complex system modeling and control, which is that high-fidelity models can be prohibitively expensive to construct. This limitation is not necessarily due to the lack of fundamental understanding of the underlying natural phenomena but due to practical constraints such as the difficulties in instrumenting the complex systems to collect relevant data, the need to resolve inherent uncertainties in the models (e.g., due to unmodeled physics), and the loss of observability due to excessive exogenous noises. The general applicability of the current solutions is hampered by the ad hoc nature of the approaches and the lack of a coherent theoretical framework. The new SciML methods developed under this project are adressing key challenges of complex systems: model construction, uncertainty quantification, decision and control, and continual learning.

The research in this project is conducted by researchers from Oak Ridge National Laboratory; Pacific Northwest National Laboratory; the University of California, Santa Barbara; and Arizona State University.

Safe Data-driven Control

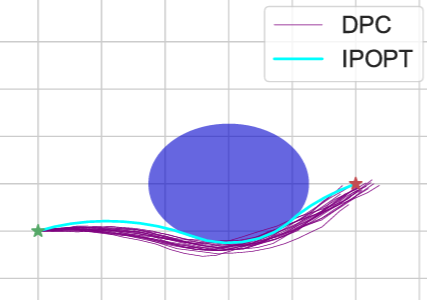
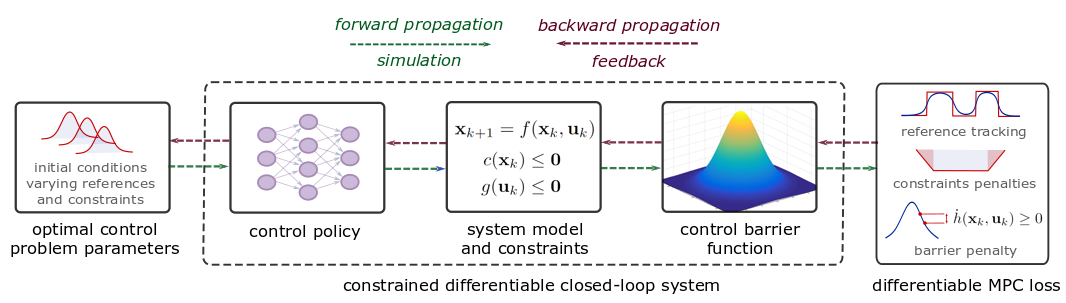
Under this project our team has developed a range of provably safe data-driven control methods based on differentiable programming paradigm. The developed methods can be used in conjunction with any learning-based controller, such as deep reinforcement learning control policy. In our case we have focused on the extensions of promissing offline model-based policy optimization approach called differentiable predictive control (DPC).

DPC is a modern SciML method that bring the benefits of both worlds. It combines model-based interpretability, constraints handling, and performance guarantees of model predictive control (MPC) with deep reinforcement learning (RL) policy optimization. This synnergy allows DPC to learn control policy parameters directly by backpropagating MPC objective function and constraints through the differentiable model of a dynamical system. Instances of a differentiable model can include a family of physics-based and data-driven differential equations models, such as neural ODEs, universal differential equations (UDEs), or neural state space models (SSMs).

Neural Lyapunov Differentiable Predictive Control combines the principles of Lyapunov functions, model predictive control, reinforcement learning, and differentiable programming to offer a systematic way for offline model-based policy optimization with guaranteed stability.

Conceptual methodology of the neural Lyapunov differentiable predictive control. Simulation of the differentiable constrained closed-loop system dynamics with neural Lyapunov function in the forward pass is followed by backward pass computing direct policy gradients for policy optimization.

Differentiable Predictive Control with Safety Guarantees: A Control Barrier Function Approach combines the principles of control barrier functions, model predictive control, reinforcement learning, and differentiable programming to offer a systematic way for offline model-based policy optimization with guaranteed constraints satisfaction via projections onto the feasible set.

Stability analysis of deep neural models

In recent years, deep neural networks (DNN) have become ever more integrated into safety-critical and high-performance systems, including robotics, autonomous driving, and process control, where formal verification methods are desired to ensure safe operation. Stability is one of the properties of dynamical systems with paramount importance for safety-verified control systems applications. To address these issues we provided sufficient conditions for i) dissipativity and ii) stochastic stability of discrete-time dynamical systems parametrized by DNNs. To do so we leverage the representation of neural networks as pointwise affine maps, thus exposing their local linear operators and making them accessible to classical system analytic and design methods. This allows us to “crack open the black box” of the neural dynamical system’s behavior. We make connections between the spectral properties of neural network’s weights and different types of used activation function on the stability and overall dynamic behavior of these type of models. Based on the theory, we propose a few practical methods for designing constrained neural dynamical models with guaranteed stability.

Dissipative neural dynamical systems: For more information read the paper

Phase portraits of deep neural dynamical system models with different stability properties and their associated eigenvalue spectra. Colors represent different initial conditions.

Stable deep markov models: For more information read the paper.

Phase portraits of stochastic neural dynamical system models with different stochastic stability properties. Thin lines are samples of the stochastic dynamics with bold lines representing mean trajectories. Colors represent different initial conditions.

Open-source Software

The technology developed under this project is being open-sourced as part of the Neuromancer Scientific Machine Learning (SciML) library developed by our team at PNNL.

PNNL Team

Acknowledgements

This project was supported through the U.S. Department of Energy (DOE), through the Office of Advanced Scientific Computing Research’s “Data-Driven Decision Control for Complex Systems (DnC2S)” project. PNNL is a multi-program national laboratory operated for the U.S. DOE by Battelle Memorial Institute under Contract No. DE-AC05-76RL0-1830.

References

2023

arXiv

Semi-Supervised Learning of Dynamical Systems with Neural Ordinary Differential Equations: A Teacher-Student Model Approach

Yu Wang, Yuxuan Yin, Karthik Somayaji Nanjangud Suryanarayana, and 5 more authors

Sep 2023

Bib

@misc{wang2023semisupervised,
  title = {{Semi-Supervised Learning of Dynamical Systems with Neural Ordinary Differential Equations:
        A Teacher-Student Model Approach}},
  author = {Wang, Yu and Yin, Yuxuan and Suryanarayana, Karthik Somayaji Nanjangud and Drgoňa, Ján and Schram, Malachi and Halappanavar, Mahantesh and Liu, Frank and Li, Peng},
  year = {2023},
  eprint = {2310.13110},
  archiveprefix = {arXiv},
  primaryclass = {cs.LG}
}

arXiv

Extreme Risk Mitigation in Reinforcement Learning using Extreme Value Theory

Karthik Somayaji NS, Yu Wang, Malachi Schram, and 4 more authors

Sep 2023

Bib

@misc{ns2023extreme,
  title = {Extreme Risk Mitigation in Reinforcement Learning using Extreme Value Theory},
  author = {NS, Karthik Somayaji and Wang, Yu and Schram, Malachi and Drgoňa, Ján and Halappanavar, Mahantesh and Liu, Frank and Li, Peng},
  year = {2023},
  eprint = {2308.13011},
  archiveprefix = {arXiv},
  primaryclass = {cs.LG}
}

AutoNF: Automated Architecture Optimization of Normalizing Flows with Unconstrained Continuous Relaxation Admitting Optimal Discrete Solution

Yu Wang, Ján Drgoňa, Jiaxin Zhang, and 4 more authors

Proceedings of the AAAI Conference on Artificial Intelligence, Jun 2023

Bib HTML

@article{AutoNF_2023,
  title = {{AutoNF: Automated Architecture Optimization of Normalizing Flows with Unconstrained
      Continuous Relaxation Admitting Optimal Discrete Solution}},
  volume = {37},
  url = {https://ojs.aaai.org/index.php/AAAI/article/view/26220},
  doi = {10.1609/aaai.v37i8.26220},
  abstractnote = {Normalizing flows (NF) build upon invertible neural networks and have wide applications in probabilistic modeling. Currently, building a powerful yet computationally efficient flow model relies on empirical fine-tuning over a large design space. While introducing neural architecture search (NAS) to NF is desirable, the invertibility constraint of NF brings new challenges to existing NAS methods whose application is limited to unstructured neural networks. Developing efficient NAS methods specifically for NF remains an open problem. We present AutoNF, the first automated NF architectural optimization framework. First, we present a new mixture distribution formulation that allows efficient differentiable architecture search of flow models without violating the invertibility constraint. Second, under the new formulation, we convert the original NP-hard combinatorial NF architectural optimization problem to an unconstrained continuous relaxation admitting the discrete optimal architectural solution, circumventing the loss of optimality due to binarization in architectural optimization. We evaluate AutoNF with various density estimation datasets and show its superior performance-cost trade-offs over a set of existing hand-crafted baselines.},
  number = {8},
  journal = {Proceedings of the AAAI Conference on Artificial Intelligence},
  author = {Wang, Yu and Drgoňa, Ján and Zhang, Jiaxin and Nanjangud Suryanarayana, Karthik Somayaji and Schram, Malachi and Liu, Frank and Li, Peng},
  year = {2023},
  month = jun,
  pages = {10244-10252}
}

2022

Differentiable Predictive Control with Safety Guarantees: A Control Barrier Function Approach

W. Shaw Cortez, Ján Drgoňa, A. Tuor, and 2 more authors

In 2022 IEEE 61st Conference on Decision and Control (CDC), Jun 2022

Bib HTML

@inproceedings{9993146,
  author = {Cortez, W. Shaw and Drgoňa, Ján and Tuor, A. and Halappanavar, M. and Vrabie, D.},
  booktitle = {2022 IEEE 61st Conference on Decision and Control (CDC)},
  title = {Differentiable Predictive Control with Safety Guarantees: A Control Barrier Function Approach},
  year = {2022},
  volume = {},
  number = {},
  url = {https://ieeexplore.ieee.org/abstract/document/9993146},
  pages = {932-938},
  doi = {10.1109/CDC51059.2022.9993146}
}

Neural Lyapunov Differentiable Predictive Control

Sayak Mukherjee, Ján Drgoňa, Aaron Tuor, and 2 more authors

In 2022 IEEE 61st Conference on Decision and Control (CDC), Dec 2022

Bib HTML Code

@inproceedings{9992386,
  author = {Mukherjee, Sayak and Drgoňa, Ján and Tuor, Aaron and Halappanavar, Mahantesh and Vrabie, Draguna},
  booktitle = {2022 IEEE 61st Conference on Decision and Control (CDC)},
  title = {Neural Lyapunov Differentiable Predictive Control},
  year = {2022},
  month = dec,
  volume = {},
  number = {},
  url = {https://ieeexplore.ieee.org/abstract/document/9992386},
  pages = {2097-2104},
  doi = {10.1109/CDC51059.2022.9992386}
}

Dissipative Deep Neural Dynamical Systems

Ján Drgoňa, Aaron Tuor, Soumya Vasisht, and 1 more author

IEEE Open Journal of Control Systems, Jun 2022

Bib HTML Code

@article{9809789,
  author = {Drgoňa, Ján and Tuor, Aaron and Vasisht, Soumya and Vrabie, Draguna},
  journal = {IEEE Open Journal of Control Systems},
  title = {Dissipative Deep Neural Dynamical Systems},
  year = {2022},
  month = jun,
  volume = {1},
  number = {},
  pages = {100-112},
  url = {https://ieeexplore.ieee.org/abstract/document/9809789},
  doi = {10.1109/OJCSYS.2022.3186838}
}

Learning Stochastic Parametric Diferentiable Predictive Control Policies

Ján Drgoňa, Sayak Mukherjee, Aaron Tuor, and 2 more authors

IFAC-PapersOnLine, Jun 2022

10th IFAC Symposium on Robust Control Design ROCOND 2022

Abs Bib HTML Code

The problem of synthesizing stochastic explicit model predictive control policies is known to be quickly intractable even for systems of modest complexity when using classical control-theoretic methods. To address this challenge, we present a scalable alternative called stochastic parametric differentiable predictive control (SP-DPC) for unsupervised learning of neural control policies governing stochastic linear systems subject to nonlinear chance constraints. SP-DPC is formulated as a deterministic approximation to the stochastic parametric constrained optimal control problem. This formulation allows us to directly compute the policy gradients via automatic differentiation of the problem’s value function, evaluated over sampled parameters and uncertainties. In particular, the computed expectation of the SP-DPC problem’s value function is back propagated through the closed-loop system rollouts parametrized by a known nominal system dynamics model and neural control policy which allows for direct model-based policy optimization. We demonstrate the computational efficiency and scalability of the proposed policy optimization algorithm in three numerical examples, including systems with a large number of states or subject to nonlinear constraints.
@article{DRGONA2022121, title = {Learning Stochastic Parametric Diferentiable Predictive Control Policies}, journal = {IFAC-PapersOnLine}, volume = {55}, number = {25}, pages = {121-126}, year = {2022}, note = {10th IFAC Symposium on Robust Control Design ROCOND 2022}, issn = {2405-8963}, doi = {https://doi.org/10.1016/j.ifacol.2022.09.334}, url = {https://www.sciencedirect.com/science/article/pii/S2405896322015877}, author = {Drgoňa, Ján and Mukherjee, Sayak and Tuor, Aaron and Halappanavar, Mahantesh and Vrabie, Draguna}, keywords = {Stochastic explicit model predictive control, offline model-based policy optimization, deep neural networks, differentiable programming, parametric programming} }

2021

On the Stochastic Stability of Deep Markov Models

Ján Drgoňa, Sayak Mukherjee, Jiaxin Zhang, and 2 more authors

In Advances in Neural Information Processing Systems, Jun 2021

Bib HTML Code

@inproceedings{NEURIPS2021_c9dd73f5,
  author = {Drgoňa, Ján and Mukherjee, Sayak and Zhang, Jiaxin and Liu, Frank and Halappanavar, Mahantesh},
  booktitle = {Advances in Neural Information Processing Systems},
  editor = {Ranzato, M. and Beygelzimer, A. and Dauphin, Y. and Liang, P.S. and Vaughan, J. Wortman},
  pages = {24033--24047},
  publisher = {Curran Associates, Inc.},
  title = {On the Stochastic Stability of Deep Markov Models},
  url = {https://proceedings.neurips.cc/paper/2021/hash/c9dd73f5cb96486f5e1e0680e841a550-Abstract.html},
  volume = {34},
  year = {2021}
}