Neuromancer SciML library

Developing novel scientific machine learning (SciML) methods and user-friendly software library in Pytorch.

Abstract

Recent research has demonstrated great advantages to integrating physical knowledge into machine learning methods, and conversely data-driven modeling into traditional physics-based scientific computing. However, the underlying compute infrastructure in the form of both hardware and software has diverged considerably from the need for integrated approaches to scientific discovery. The current misalignment of these sets of tools has led to some very inefficient scientific workflows involving running computations on different systems, transposition of data between formats and expensive data copies (in both time and space). As well, the lack of tight integration, directly results in slower computations and methodological limitations (e.g. impractical to solve end-to-end optimization problems across scientific computing and machine learning codes).

To adress these issues, this project developed novel principled scientific machine learning (SciML) methods and software tools. Specifically, under this project our team at PNNL has developed NeuroMANCER SciML library in Pytorch.

Open-source Software

Neural Modules with Adaptive Nonlinear Constraints and Efficient Regularizations (NeuroMANCER) is an open-source differentiable programming (DP) library for solving parametric constrained optimization problems, physics-informed system identification, and parametric model-based optimal control. NeuroMANCER is written in PyTorch and allows for systematic integration of machine learning with scientific computing for creating end-to-end differentiable models and algorithms embedded with prior knowledge and physics.

SciML Methods in Neuromancer

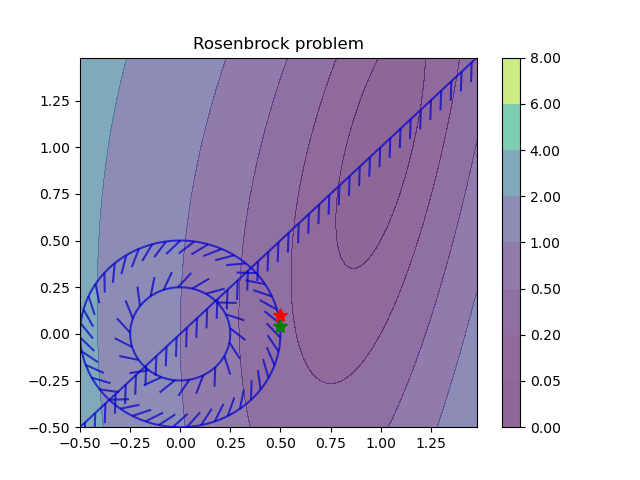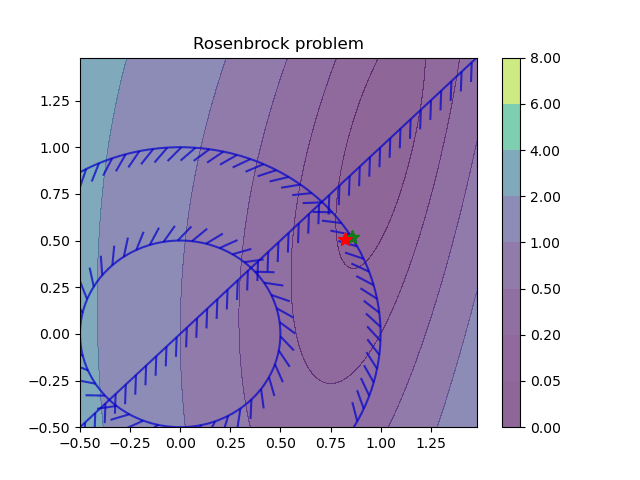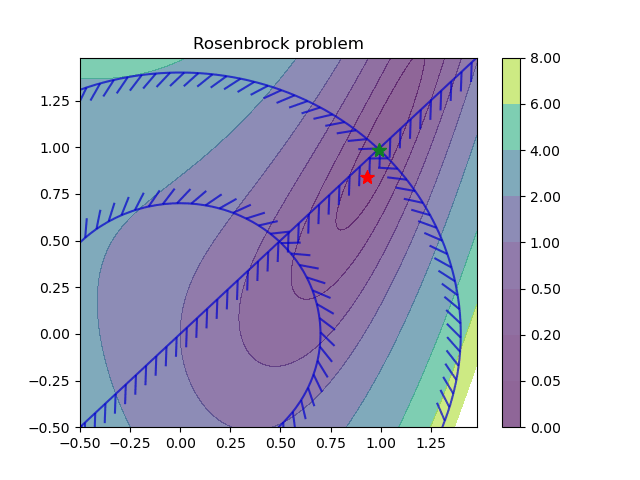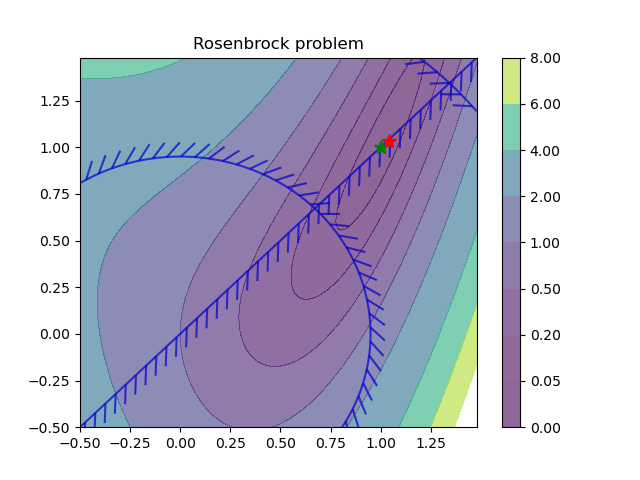
Learning to optimize (L2O) for constrained optimization

Learning Solutions to Constrained Optimization Problems is a set of methods that use machine learning to learn the
solutions (explicit solvers) to optimization problems. Constrained optimization problems where the solution x depends on the varying problem parameters ξ are called parametric programming problems. Neuromancer allows you to formulate and solve a broad class of parametric optimization problems via the Differentiable Programming (DP) paradigm. Hence, we call the approach Differentiable Programming Programming (DPP). Specifically, Neuromancer allows you to use automatic differentiation (AD) in PyTorch to compute the sensitivities of such constrained optimization problems w.r.t. their parameters. This allows you to leverage gradient-based optimizers (e.g., stochastic gradient descent) to obtain approximate solutions to constrained parametric programming problems via for semi-supervised offline learning. The main advantage of this offline DPP-based solution compared to classical optimization solvers (e.g., IPOPT) is faster online evaluation, often obtaining orders of magnitude speedups.

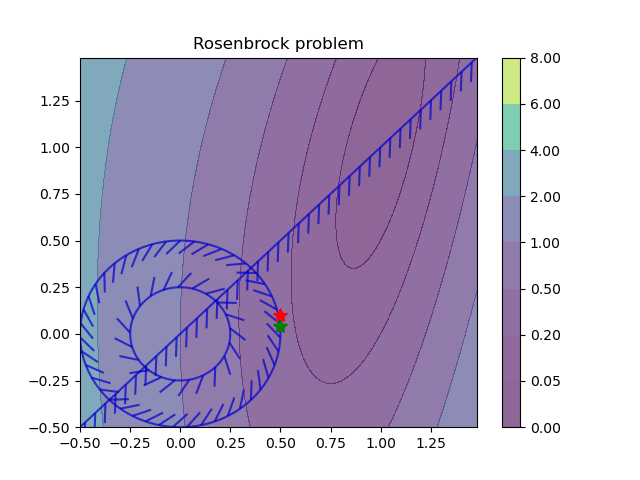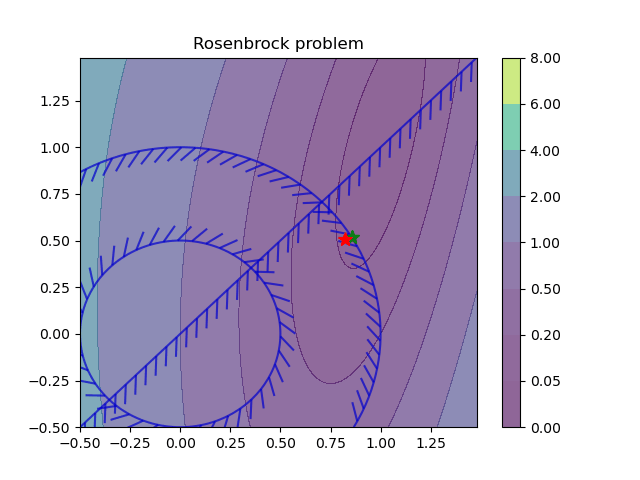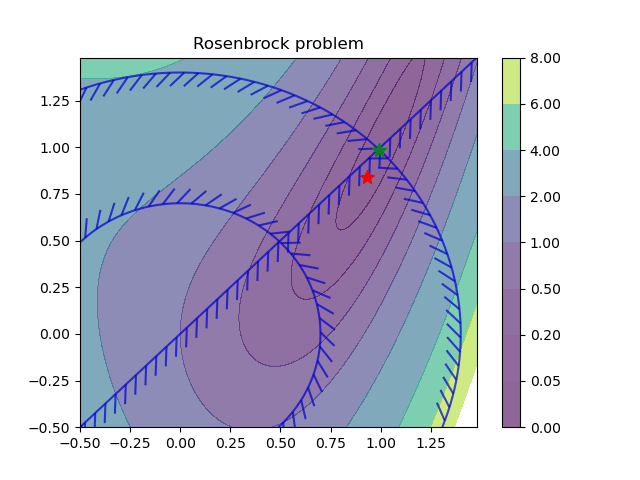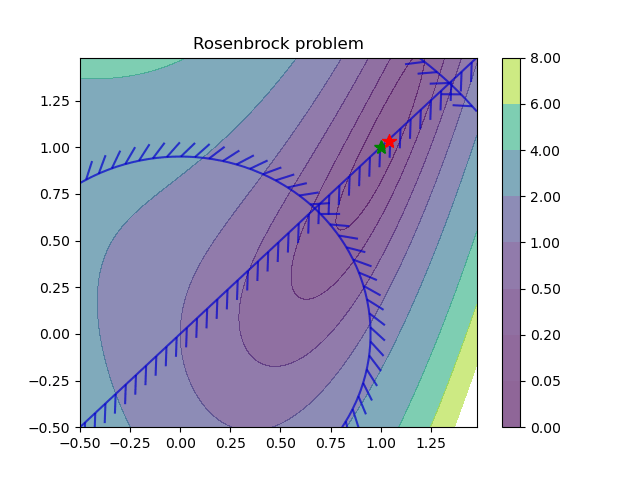
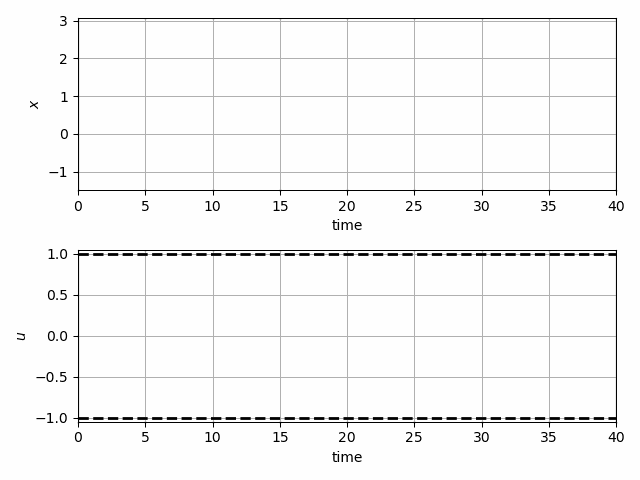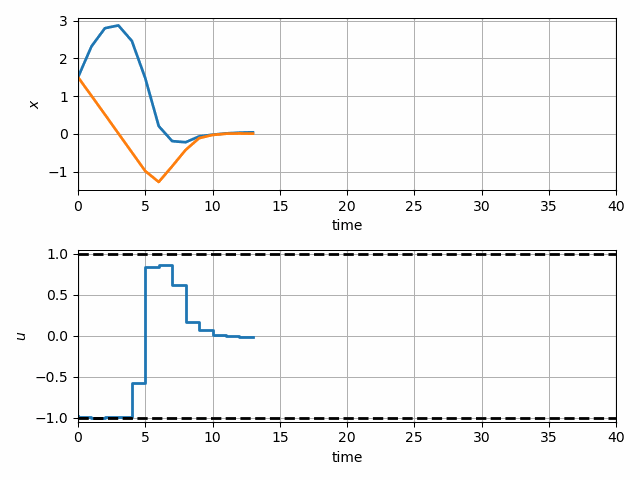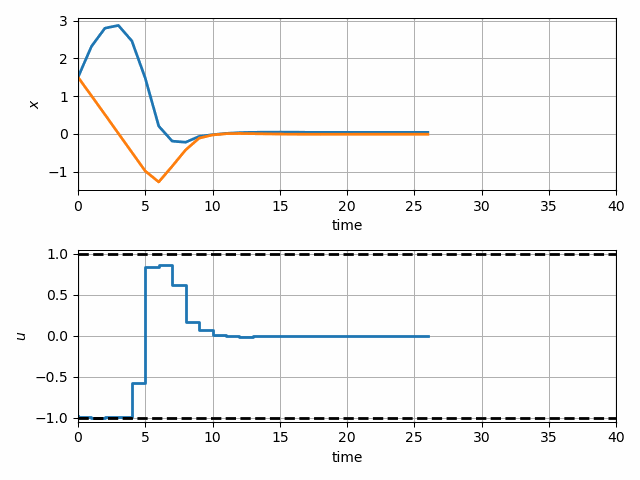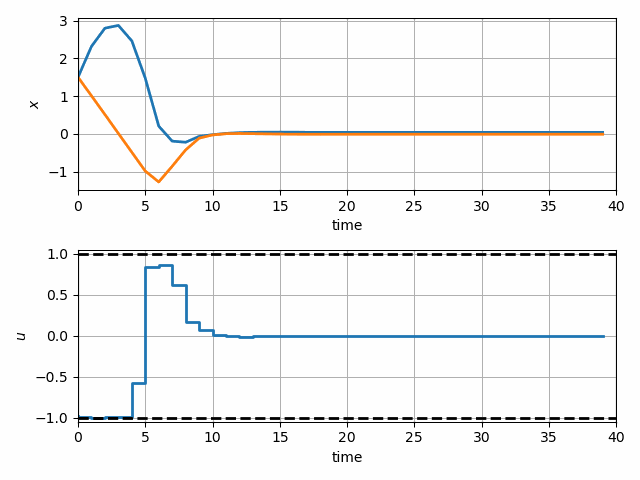
For more information see the open-source examples.

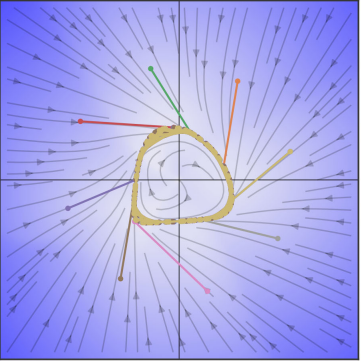
Learning SciML surrogates for dynamical systems

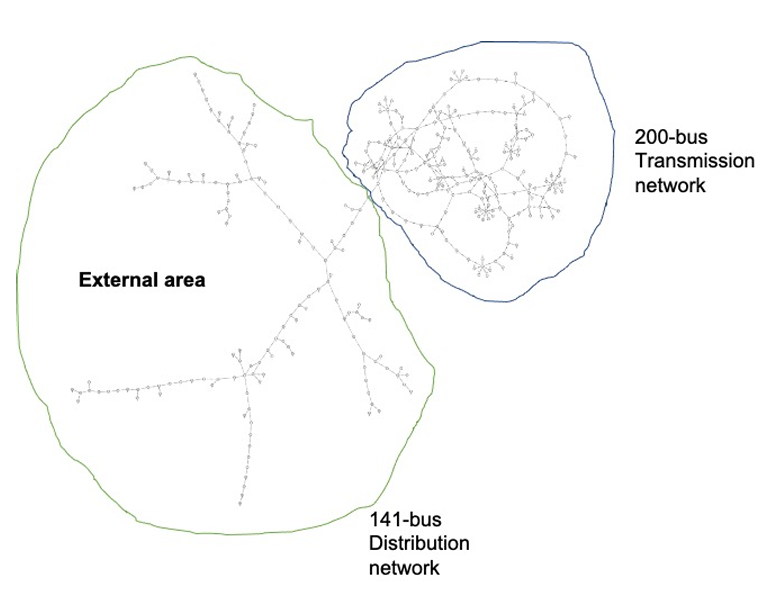
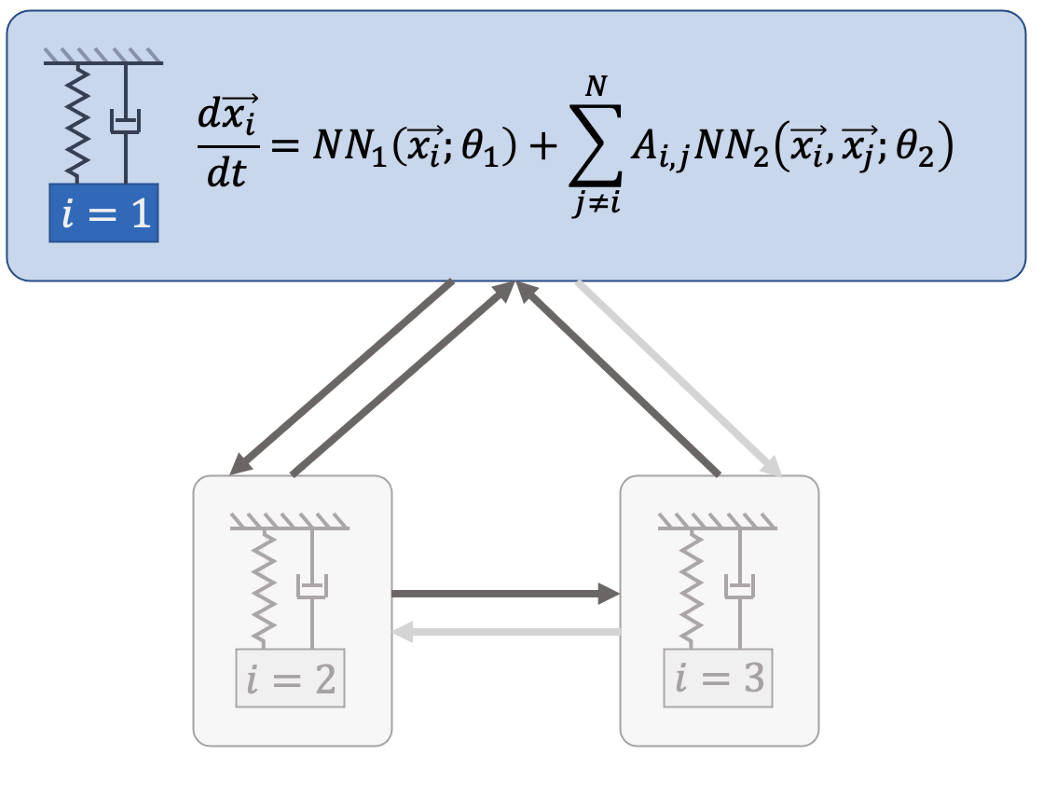
System identification is using statistical methods to construct mathematical models of dynamical systems given the measured observations of the system behavior. In the Neuromancer library, we are primarily interested in differentiable system ID methods that can incorporate prior physical knowledge into their architectures and loss functions. Examples include structural assumption on the computational graph inspired by domain application, structure of the weight matrices, or network architectures. Differentiaity allows us to leverage gradient-based optimization algorithms for learning the unknown parameters of these structured digital twin models from observational data of the real system.

Neuromancer currently supports the following system identification methods:

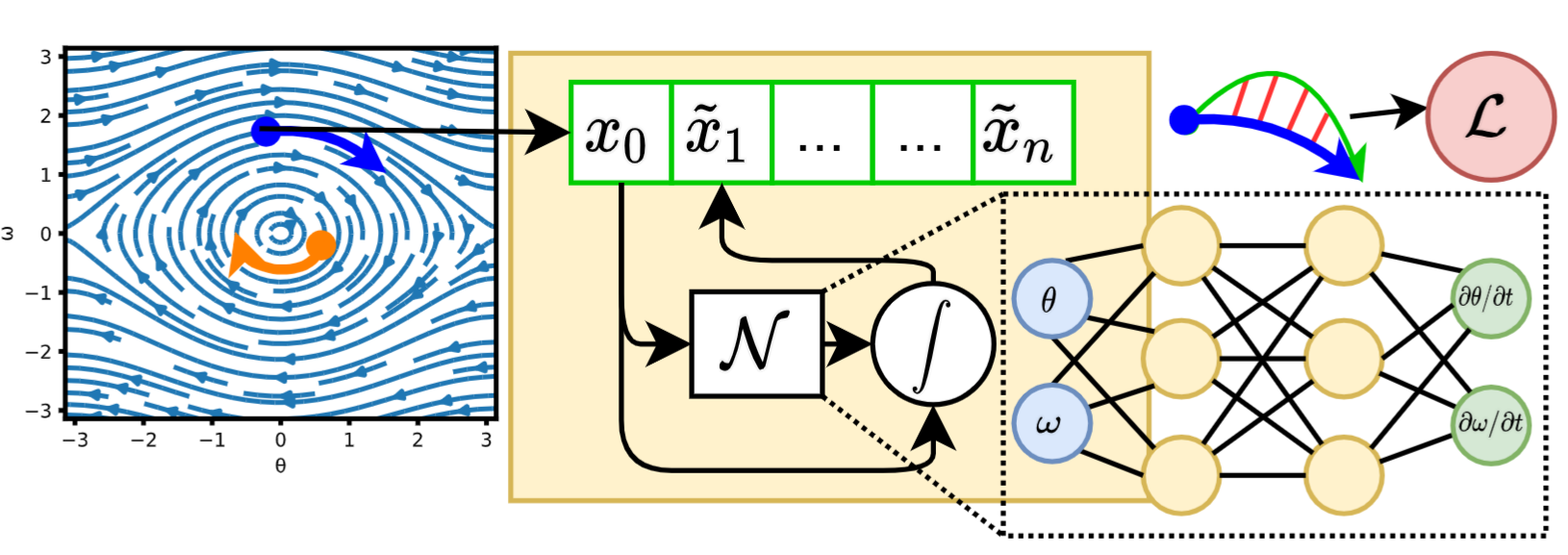
For more information see the open-source examples

Learning to control with differentiable programming

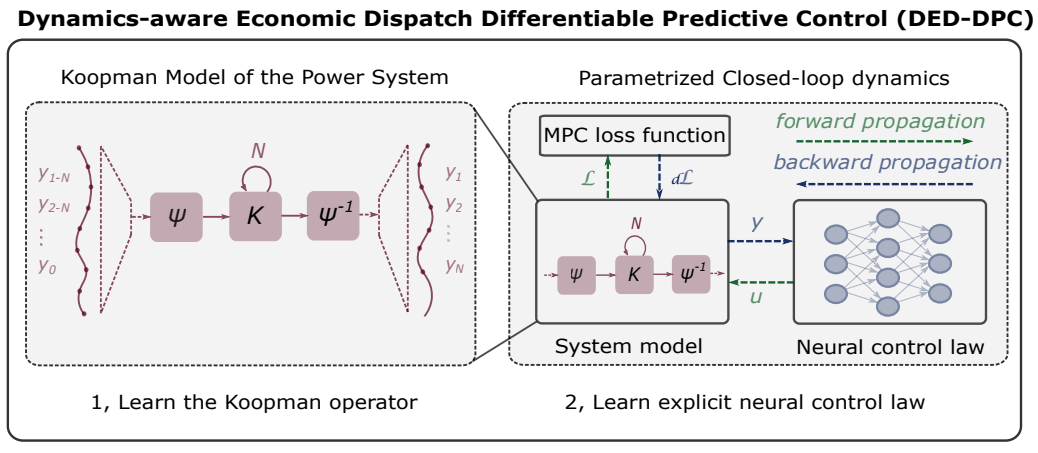
Differentiable predictive control (DPC) method represents a flagship capability of the Neuromancer library.

DPC allows us to learn control policy parameters directly by backpropagating model predictive control (MPC) objective function and constraints through the differentiable model of a dynamical system. Instances of a differentiable model include ordinary differential equations (ODEs), including neural ODEs, universal differential equations (UDEs), or neural state space models (SSMs).

The conceptual methodology shown in the figures below consists of two main steps. In the first step, we perform system identification by learning the unknown parameters of differentiable digital twins. In the second step, we close the loop by combining the digital twin models with control policy, parametrized by neural networks, obtaining a differentiable closed-loop dynamics model. This closed-loop model now allow us to use automatic differentiation (AD) to solve the parametric optimal control problem by computing the sensitivities of objective functions and constraints to changing problem parameters such as initial conditions, boundary conditions, and parametric control tasks such as time-varying reference tracking.

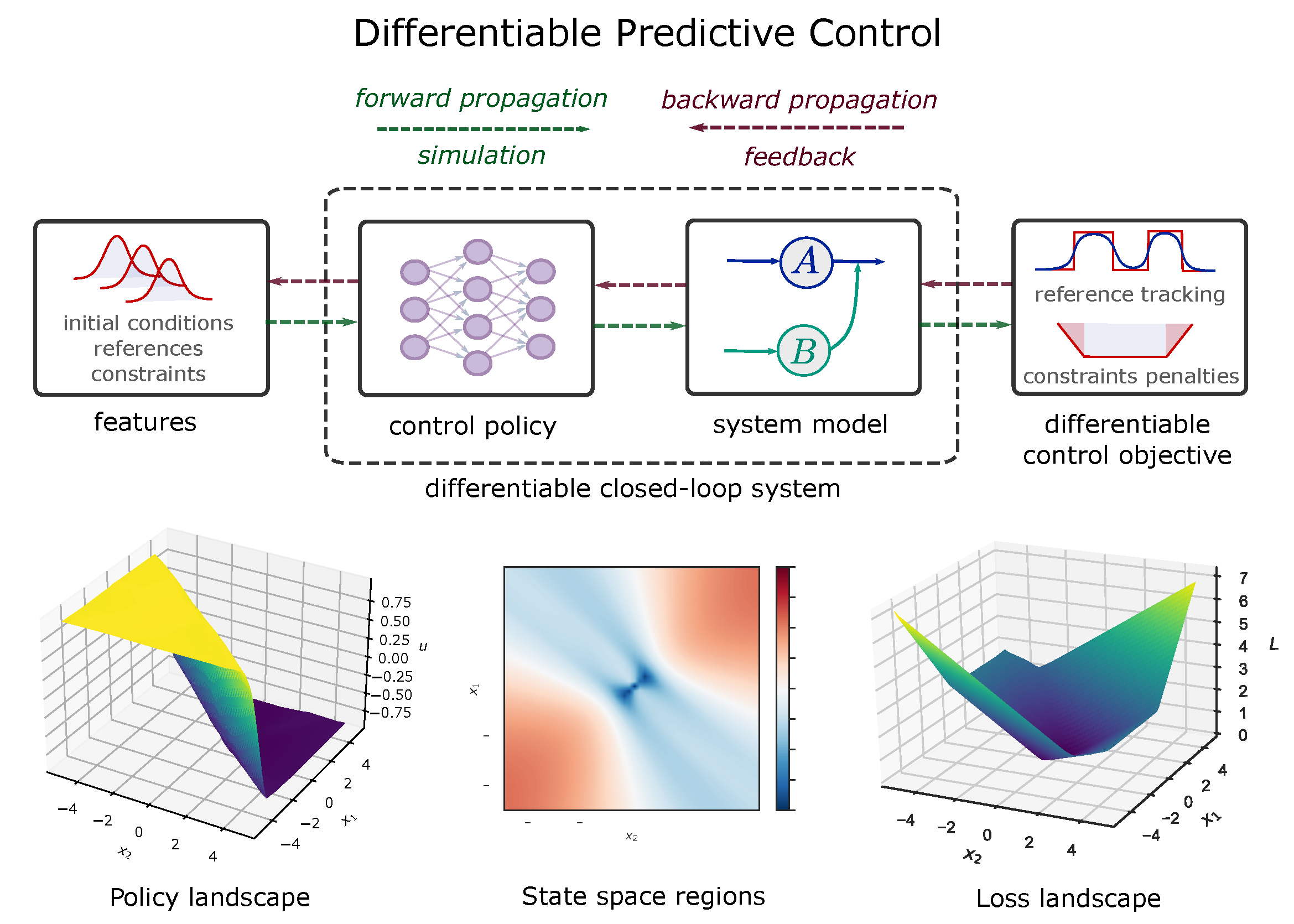
For more information see the open-source examples

Active Core Developers Team

Ján Drgoňa (PI)
Rahul Birmiwal
Bruno Jacob
Draguna Vrabie (Main Scientific Advisor)

Contributors and Collaborators

Aaron Tuor (Co-PI)
Madelyn Shapiro
James Koch
Cary Faulkner
Ethan King
Zhao Chen
Shrirang Abhyankar
Mia Skomski
Christian Møldrup Legaard (Aarhus University - Summer internship)
Bo Tang (UToronto - Summer internship)
James Kotary (UVA - Summer internship)
Cody Beck (NAU - Summer internship)
Nandan Tumu (UPenn - Summer internship)
Seth Britney (WWU - Summer internship)

Acknowledgements

This research was partially supported by the Mathematics for Artificial Reasoning in Science (MARS) and Data Model Convergence (DMC) initiatives via the Laboratory Directed Research and Development (LDRD) investments at Pacific Northwest National Laboratory (PNNL). PNNL is a multi-program national laboratory operated for the U.S. Department of Energy (DOE) by Battelle Memorial Institute under Contract No. DE-AC05-76RL0-1830.

References

2023

Neuro-physical dynamic load modeling using differentiable parametric optimization

Shrirang Abhyankar, Ján Drgoňa, Aaron Tuor, and 1 more author

In 2023 IEEE Power & Energy Society General Meeting (PESGM), 2023

Bib HTML

@inproceedings{10253098,
  author = {Abhyankar, Shrirang and Drgoňa, Ján and Tuor, Aaron and August, Andrew},
  booktitle = {2023 IEEE Power & Energy Society General Meeting (PESGM)},
  title = {Neuro-physical dynamic load modeling using differentiable parametric optimization},
  year = {2023},
  volume = {},
  number = {},
  pages = {1-5},
  doi = {10.1109/PESGM52003.2023.10253098},
}

ACM e-Energy
Power Grid Behavioral Patterns and Risks of Generalization in Applied Machine Learning

Shimiao Li, Ján Drgoňa, Shrirang Abhyankar, and 1 more author

In Companion Proceedings of the 14th ACM International Conference on Future Energy Systems, 2023

Abs Bib HTML

Recent years have seen a rich literature of data-driven approaches designed for power grid applications. However, insufficient consideration of domain knowledge can impose a high risk to the practicality of the methods. Specifically, ignoring the grid-specific spatiotemporal patterns (in load, generation, and topology, etc.) can lead to outputting infeasible, unrealizable, or completely meaningless predictions on new inputs. To address this concern, this paper investigates real-world operational data to provide insights into power grid behavioral patterns, including the time-varying topology, load, and generation, as well as the spatial differences (in peak hours, diverse styles) between individual loads and generations. Then based on these observations, we evaluate the generalization risks in some existing ML works caused by ignoring these grid-specific patterns in model design and training.
@inproceedings{Shimiao2023, author = {Li, Shimiao and Drgoňa, Ján and Abhyankar, Shrirang and Pileggi, Larry}, title = {Power Grid Behavioral Patterns and Risks of Generalization in Applied Machine Learning}, year = {2023}, isbn = {9798400702273}, publisher = {Association for Computing Machinery}, address = {New York, NY, USA}, url = {https://doi.org/10.1145/3599733.3600257}, doi = {10.1145/3599733.3600257}, booktitle = {Companion Proceedings of the 14th ACM International Conference on Future Energy Systems}, pages = {106–114}, numpages = {9}, keywords = {domain knowledge, power grid, generalization, machine learning}, location = {Orlando, FL, USA}, series = {e-Energy '23 Companion} }
Constructing Neural Network Based Models for Simulating Dynamical Systems

Christian Legaard, Thomas Schranz, Gerald Schweiger, and 6 more authors

ACM Computing Surveys, Feb 2023

Abs Bib HTML Code

Dynamical systems see widespread use in natural sciences like physics, biology, and chemistry, as well as engineering disciplines such as circuit analysis, computational fluid dynamics, and control. For simple systems, the differential equations governing the dynamics can be derived by applying fundamental physical laws. However, for more complex systems, this approach becomes exceedingly difficult. Data-driven modeling is an alternative paradigm that seeks to learn an approximation of the dynamics of a system using observations of the true system. In recent years, there has been an increased interest in applying data-driven modeling techniques to solve a wide range of problems in physics and engineering. This article provides a survey of the different ways to construct models of dynamical systems using neural networks. In addition to the basic overview, we review the related literature and outline the most significant challenges from numerical simulations that this modeling paradigm must overcome. Based on the reviewed literature and identified challenges, we provide a discussion on promising research areas.
@article{Legaard2023, author = {Legaard, Christian and Schranz, Thomas and Schweiger, Gerald and Drgo\v{n}a, J\'{a}n and Falay, Basak and Gomes, Cl\'{a}udio and Iosifidis, Alexandros and Abkar, Mahdi and Larsen, Peter}, title = {Constructing Neural Network Based Models for Simulating Dynamical Systems}, year = {2023}, issue_date = {November 2023}, publisher = {Association for Computing Machinery}, address = {New York, NY, USA}, volume = {55}, number = {11}, issn = {0360-0300}, url = {https://doi.org/10.1145/3567591}, doi = {10.1145/3567591}, journal = {ACM Computing Surveys}, month = feb, articleno = {236}, numpages = {34}, keywords = {physics-informed neural networks, physics-based regularization, Neural ODEs} }
Structural inference of networked dynamical systems with universal differential equations

J. Koch, Z. Chen, A. Tuor, and 2 more authors

Chaos: An Interdisciplinary Journal of Nonlinear Science, Feb 2023

Abs Bib HTML

Networked dynamical systems are common throughout science in engineering; e.g., biological networks, reaction networks, power systems, and the like. For many such systems, nonlinearity drives populations of identical (or near-identical) units to exhibit a wide range of nontrivial behaviors, such as the emergence of coherent structures (e.g., waves and patterns) or otherwise notable dynamics (e.g., synchrony and chaos). In this work, we seek to infer (i) the intrinsic physics of a base unit of a population, (ii) the underlying graphical structure shared between units, and (iii) the coupling physics of a given networked dynamical system given observations of nodal states. These tasks are formulated around the notion of the Universal Differential Equation, whereby unknown dynamical systems can be approximated with neural networks, mathematical terms known a priori (albeit with unknown parameterizations), or combinations of the two. We demonstrate the value of these inference tasks by investigating not only future state predictions but also the inference of system behavior on varied network topologies. The effectiveness and utility of these methods are shown with their application to canonical networked nonlinear coupled oscillators.
@article{KochChaos2023, author = {Koch, J. and Chen, Z. and Tuor, A. and Drgoňa, Ján and Vrabie, D.}, title = {{Structural inference of networked dynamical systems with universal differential equations}}, journal = {Chaos: An Interdisciplinary Journal of Nonlinear Science}, volume = {33}, number = {2}, pages = {023103}, year = {2023}, month = feb, issn = {1054-1500}, doi = {10.1063/5.0109093}, url = {https://doi.org/10.1063/5.0109093}, eprint = {https://pubs.aip.org/aip/cha/article-pdf/doi/10.1063/5.0109093/16958339/023103\_1\_5.0109093.pdf} }

Homotopy Learning of Parametric Solutions to Constrained Optimization Problems

Shimiao Li, Ján Drgoňa, Aaron R Tuor, and 2 more authors

Feb 2023

Bib HTML

@misc{li2023homotopy,
  title = {Homotopy Learning of Parametric Solutions to Constrained Optimization Problems},
  author = {Li, Shimiao and Drgoňa, Ján and Tuor, Aaron R and Pileggi, Larry and Vrabie, Draguna L},
  year = {2023},
  url = {https://openreview.net/forum?id=GdimRqV_S7}
}

2022

Dissipative Deep Neural Dynamical Systems

Ján Drgoňa, Aaron Tuor, Soumya Vasisht, and 1 more author

IEEE Open Journal of Control Systems, Jun 2022

Bib HTML Code

@article{9809789,
  author = {Drgoňa, Ján and Tuor, Aaron and Vasisht, Soumya and Vrabie, Draguna},
  journal = {IEEE Open Journal of Control Systems},
  title = {Dissipative Deep Neural Dynamical Systems},
  year = {2022},
  month = jun,
  volume = {1},
  number = {},
  pages = {100-112},
  url = {https://ieeexplore.ieee.org/abstract/document/9809789},
  doi = {10.1109/OJCSYS.2022.3186838}
}

Koopman-based Differentiable Predictive Control for the Dynamics-Aware Economic Dispatch Problem

Ethan King, Ján Drgoňa, Aaron Tuor, and 4 more authors

In 2022 American Control Conference (ACC), Jun 2022

Bib HTML Code

@inproceedings{9867379,
  author = {King, Ethan and Drgoňa, Ján and Tuor, Aaron and Abhyankar, Shrirang and Bakker, Craig and Bhattacharya, Arnab and Vrabie, Draguna},
  booktitle = {2022 American Control Conference (ACC)},
  title = {Koopman-based Differentiable Predictive Control for the Dynamics-Aware Economic Dispatch Problem},
  year = {2022},
  volume = {},
  number = {},
  pages = {2194-2201},
  url = {https://ieeexplore.ieee.org/abstract/document/9867379},
  doi = {10.23919/ACC53348.2022.9867379}
}

ACC

Neural Ordinary Differential Equations for Nonlinear System Identification

Aowabin Rahman, Ján Drgoňa, Aaron Tuor, and 1 more author

In 2022 American Control Conference (ACC), Jun 2022

Bib HTML Code

@inproceedings{9867586,
  author = {Rahman, Aowabin and Drgoňa, Ján and Tuor, Aaron and Strube, Jan},
  booktitle = {2022 American Control Conference (ACC)},
  title = {Neural Ordinary Differential Equations for Nonlinear System Identification},
  year = {2022},
  volume = {},
  number = {},
  pages = {3979-3984},
  url = {https://ieeexplore.ieee.org/abstract/document/9867586},
  doi = {10.23919/ACC53348.2022.9867586}
}

Learning Constrained Adaptive Differentiable Predictive Control Policies With Guarantees

Ján Drgoňa, Aaron Tuor, and Draguna Vrabie

Jun 2022

arXiv Bib Code

@misc{drgona2022learning,
  title = {Learning Constrained Adaptive Differentiable Predictive Control Policies With Guarantees},
  author = {Drgoňa, Ján and Tuor, Aaron and Vrabie, Draguna},
  year = {2022},
  eprint = {2004.11184},
  archiveprefix = {arXiv},
  primaryclass = {eess.SY}
}

2021

L4DC

Automating Discovery of Physics-Informed Neural State Space Models via Learning and Evolution

Elliott Skomski, Ján Drgoňa, and Aaron Tuor

In Proceedings of the 3rd Conference on Learning for Dynamics and Control, 07 – 08 june 2021

Bib HTML PDF

@inproceedings{skomski21a,
  title = {Automating Discovery of Physics-Informed Neural State Space Models via Learning and Evolution},
  author = {Skomski, Elliott and Drgo\v{n}a, J\'an and Tuor, Aaron},
  booktitle = {Proceedings of the 3rd Conference on Learning for Dynamics and Control},
  pages = {980--991},
  year = {2021},
  editor = {Jadbabaie, Ali and Lygeros, John and Pappas, George J. and A.&nbsp;Parrilo, Pablo and Recht, Benjamin and Tomlin, Claire J. and Zeilinger, Melanie N.},
  volume = {144},
  series = {Proceedings of Machine Learning Research},
  month = {07 -- 08 June},
  publisher = {PMLR},
  url = {https://proceedings.mlr.press/v144/skomski21a.html},
  abs = {Recent works exploring deep learning application to dynamical systems modeling have demonstrated that embedding physical priors into neural networks can yield more effective, physically-realistic, and data-efficient models. However, in the absence of complete prior knowledge of a dynamical system’s physical characteristics, determining the optimal structure and optimization strategy for these models can be difficult. In this work, we explore methods for discovering neural state space dynamics models for system identification. Starting with a design space of block-oriented state space models and structured linear maps with strong physical priors, we encode these components into a model genome alongside network structure, penalty constraints, and optimization hyperparameters. Demonstrating the overall utility of the design space, we employ an asynchronous genetic search algorithm that alternates between model selection and optimization and obtains accurate physically consistent models of three physical systems: an aerodynamics body, a continuous stirred tank reactor, and a two tank interacting system.}
}

Constrained Block Nonlinear Neural Dynamical Models

Elliott Skomski, Soumya Vasisht, Colby Wight, and 3 more authors

In 2021 American Control Conference (ACC), 07 – 08 june 2021

Bib HTML Code

@inproceedings{SkomskiACC2021,
  author = {Skomski, Elliott and Vasisht, Soumya and Wight, Colby and Tuor, Aaron and Drgoňa, Ján and Vrabie, Draguna},
  booktitle = {2021 American Control Conference (ACC)},
  title = {Constrained Block Nonlinear Neural Dynamical Models},
  year = {2021},
  volume = {},
  number = {},
  pages = {3993-4000},
  url = {https://ieeexplore.ieee.org/abstract/document/9482930},
  doi = {10.23919/ACC50511.2021.9482930}
}

2020

ICLR

Constrained Neural Ordinary Differential Equations with Stability Guarantees

Aaron Tuor, Ján Drgoňa, and Draguna Vrabie

07 – 08 june 2020

arXiv Bib Code

@misc{tuor2020constrained,
  title = {Constrained Neural Ordinary Differential Equations with Stability Guarantees},
  author = {Tuor, Aaron and Drgoňa, Ján and Vrabie, Draguna},
  year = {2020},
  eprint = {2004.10883},
  archiveprefix = {arXiv},
  url = {https://arxiv.org/abs/2004.10883},
  primaryclass = {eess.SY}
}